Calculus Using the First and Second Derivative Tests, find all relative maxima and minima of the function f(x) = x^2 6x^{4/3}The second derivative of the function x2 y2 =25 is equal to (25/y3) True or false?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
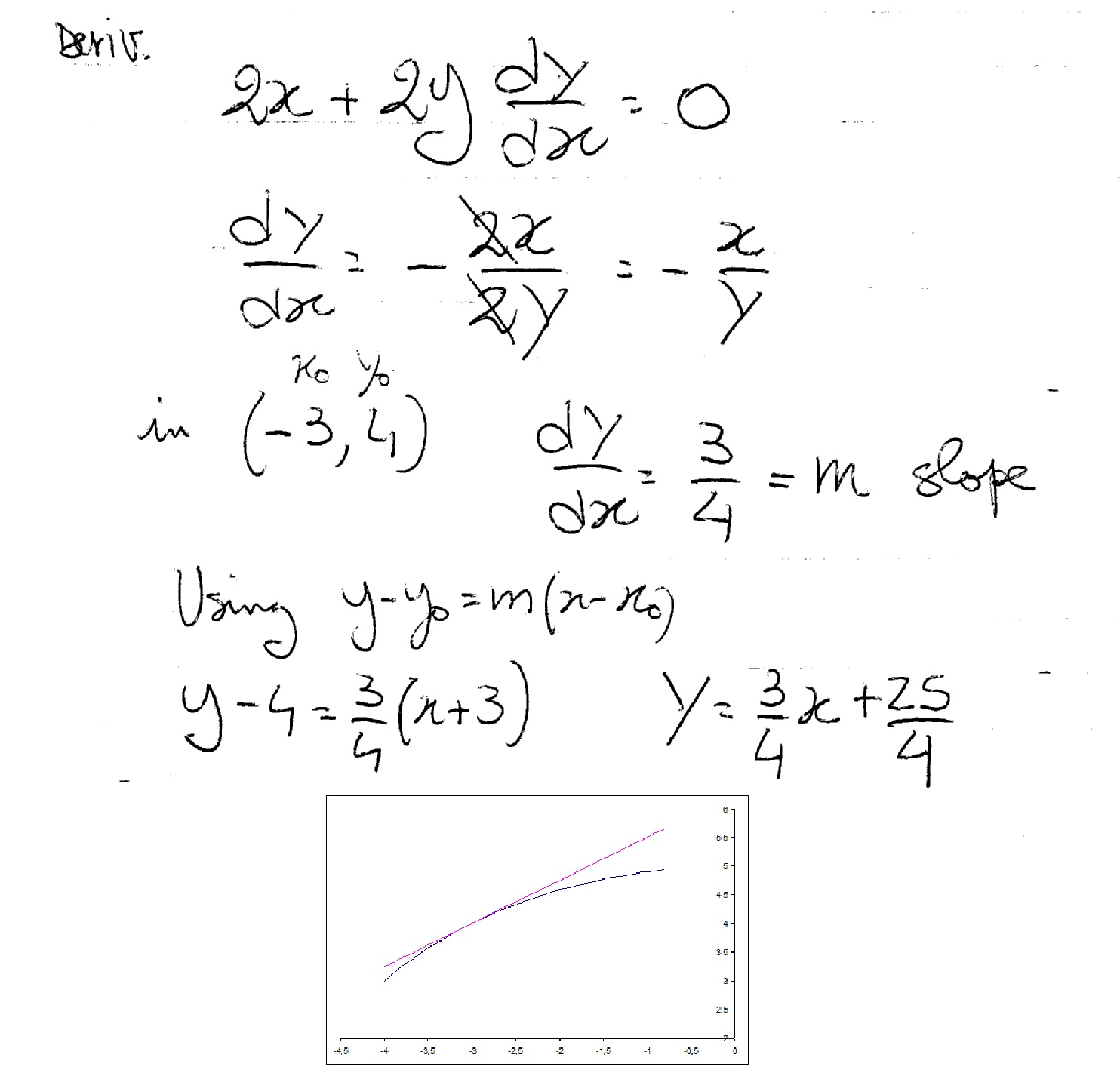
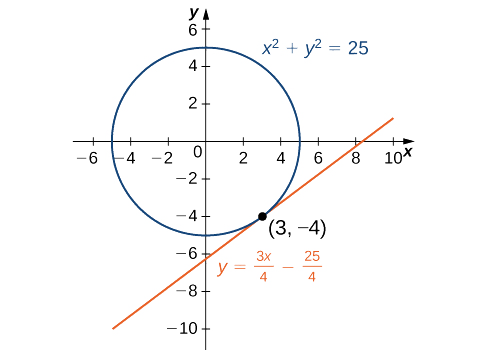
How Do You Find Equation Of Tangent To Circle X 2 Y 2 25 At The Point 3 4 Socratic
X^2+y^2=25 second derivative
X^2+y^2=25 second derivative-If the second derivative is greater than zero, the stationary point is a minimum If the second derivative equals zero, the stationary point could be a point of inflection The derivative of a curve is found to be g ′ (x) = 4 x 2 − 7 2 x g'(x) = 4x^2 \frac{7}{2}x g ′ (x) = 4 x 2 − 2 7 xWe have to evaluate the first and second derivative of the function, {eq}\bullet \;



Implicit Differentiation Notes Cocalc
$x^2y^2=25$,consider a very magnified neighbourhood of the curve at any point excepts the points $x=5,5$In that neighbourhood there can be defined as function $f$ such that $y=f(x)$ where $y$ satisfies the given relationNow express $y$ in terms of $x$Take one of $f(x)=\sqrt{(25x^2)}$ or $f(x)=\sqrt{25x^2}$then differentiate like a function,you willX 2 y 2 = 25 , y 2 = 25 x 2, and , where the positive square root represents the top semicircle and the negative square root represents the bottom semicircle Since the point (3, 4) lies on the bottom semicircle given by , the derivative of y is , ie, Thus, the slope of the line tangent to the graph at the point (3, 4) isDifferentiate using the Power Rule which states that d dx xn d d x x n is nxn−1 n x n 1 where n = 2 n = 2 Since y2 y 2 is constant with respect to x x, the derivative of y2 y 2 with respect to x x is 0 0 Simplify terms Tap for more steps Add 2 x 2 x and 0 0
The Derivative Calculator supports computing first, second, , fifth derivatives as well as differentiating functions with many variables (partial derivatives), implicit differentiation and calculating roots/zeros You can also check your answers!Textbook solution for Calculus (MindTap Course List) 11th Edition Ron Larson Chapter 25 Problem 51E We have stepbystep solutions for your textbooks written by Bartleby experts!Let's say that we're given the equation that y squared minus x squared is equal to four and our goal is to find the second derivative of Y with respect to X and we want to find an expression for it in terms of X's and Y's so pause this video and see if you can work through this alright now let's do it together now some of you might have wanted to solve for y and then use some traditional
Interactive graphs/plots help visualize and better understand the functionsFind the 2nd Derivative x^2y^225 Find the first derivative Tap for more steps By the Sum Rule, the derivative of with respect to is Find the second derivative Tap for more steps Since is constant with respect to , the derivative of with respect to isExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the



Numeracy Maths And Statistics Academic Skills Kit




Difrentiation Phpapp01
Derivative of (25/x) Derivative of (25/x) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processFind the 2nd Derivative e^(x^2) Find the first derivative Tap for more steps Differentiate using the chain rule, which states that is where and Find the second derivative Tap for more steps Since is constant with respect to , the derivative of with respect to isExpert Answer Who are the experts?




Chapter 16 Partial Differentiation




Objectives 1 Be Able To Determine If An Equation Is In Explicit Form Or Implicit Form 2 Be Able To Find The Slope Of Graph Using Implicit Differentiation Ppt Download
Derivatives › Second Derivative Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Mean, Median & Mode Scientific Notation Arithmetics Algebra Finding the first derivative of the function x 2 y 2 = 4 gives you y ′ = − x y Then to find the 2nd derivative you apply the quotient rule, which looks like this y ″ = y ( − 1) − ( − x) y ′ y 2 which gives you − y x y ′ y 2 But after looking in the back of the book I realized my answer was wrong calculus implicit 1) Find the second derivative of x^2 y ^ 2 = 25 I can only find the first derivative i can't find the second 2) Find the second derivative of y = x^2 y^3 xy I actually have no clue how to find the second derviative This sort of question is going to be on a test, but my teacher didn't cover it So please explain it step by step



Implicit Differentiation




3 Derivatives Derivatives The Functions That We Have
Example problem in higher derivativesThe second derivative of an implicit function can be found using sequential differentiation of the initial equation F (x,y) = 0 At the first step, we get the first derivative in the form y′ = f 1(x,y) On the next step, we find the second derivative, which can be expressed in terms of the variables x and y as y′′ = f 2(x,y)This question, as asked, doesn't really make sense An equation doesn't have a derivative, functions have derivatives If we claim that mathy/math is a function of mathx/math, and that ma
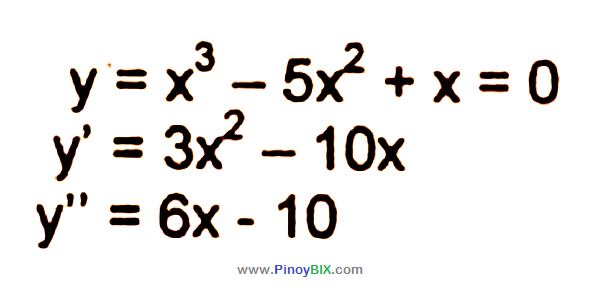



Solution Find The Second Derivative Of X 3 5x 2 X 0



4 2 Implicit Differentiation
Derivative of 25((x^2)(y^2)) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkF(x)=\dfrac{\ln x}{x^2} {/eq} The function is a quotient where we can identify,Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder derivatives Note for secondorder derivatives, the notation is often used At a point , the derivative is defined to be




1 Use Implicit Differentiation To Find Dy Dx If Xy Chegg Com




Solution What Is The Equation Of The Normal To The Curve X 2 Y
Learn how to solve implicit differentiation problems step by step online Find the implicit derivative (d/dx)(x^2y^2=25) Apply implicit differentiation by taking the derivative of both sides of the equation with respect to the differentiation variable The derivative of the constant function (25) is equal to zero The derivative of a sum of two functions is the sum of the derivatives of eachThe second derivative is the derivative of the derivative of a function, when it is defined It makes it possible to measure changes in the rates of change For example, the second derivative of the displacement is the variation of the speed (rate of variation ofCalculus Find the Second Derivative x^2y^2=25 x2 − y2 = 25 x 2 y 2 = 25 Since 25 25 is constant with respect to x x, the derivative of 25 25 with respect to x x is 0 0 f '(x) = 0 f ′ ( x) = 0 Since 0 0 is constant with respect to x x, the derivative of 0 0 with respect to x x is 0 0




Implicit Differentiation



Www3 Nd Edu Apilking Math Lectures 11 implicit differentiation Pdf
I know it should be $\frac {3}{4}\sec^3(t)$ and is concave upward whenever that expression is positive, but I don't know how to get thereY = sqrt(x^2 1), Find the first and second derivatives of the function The Derivative of x^2 We want the derivative of x^2 at an arbitrary value of x to measure the (instantaneous) rate of change of the function at that point This is also described as the slope of the tangent line to the graph of at that point Start by picking an arbitrary value of Then let be a nonzero number




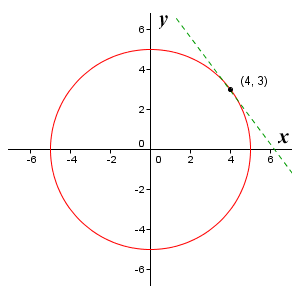
Solution What Is The Equation Of The Normal To The Curve X 2 Y 2 25 At 4 3




Difrentiation Phpapp01
What is the second derivative of {eq}x^2y^2 =25{/eq} Implicit differentiation It is not always necessary to rewrite an equation explicitly to derive it We can use a procedure called implicitFirst recall that 2^x = e^(x*ln 2) Now apply the chain rule to this function using u = x * ln 2 d/dx(e^u) = e^u * (du/dx) With u = x * ln 2, du/dx = ln 2 So d/dx(e^u) = ln 2 * e^u = ln 2 * e^(x ln 2) = ln 2 * 2^x, if you prefer it that way IFor example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of
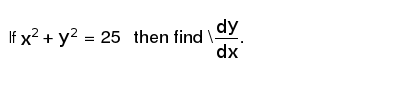



If X 2 Y 2 25 Then Find Dy Dx




Worked Example Implicit Differentiation Video Khan Academy
Remember that the derivative of y with respect to x is written dy/dx The second derivative is written d 2 y/dx 2, pronounced "dee two y by d x squared" Stationary Points The second derivative can be used as an easier way of determining the nature of stationary points (whether they are maximum points, minimum points or points of inflection)Textbook solution for Calculus of a Single Variable 11th Edition Ron Larson Chapter 25 Problem 49E We have stepbystep solutions for your textbooks written by Bartleby experts!Learn how to solve implicit differentiation problems step by step online Find the implicit derivative (d/dx)(x^2y^2z^2=25) Apply implicit differentiation by taking the derivative of both sides of the equation with respect to the differentiation variable The derivative of the constant function (25) is equal to zero The derivative of a sum of two functions is the sum of the derivatives of




X 2 Y 2 25 Novocom Top




3 Derivatives Derivatives The Functions That We Have
Derivative of 25(x^2y^2) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving processGet the detailed answer Find the second derivative d^2y/dx^2 as a function of x and y x^2 y^2 = 25 2 Find the equation of tangent to the graph of y Free unlimited access forSecond order derivatives Bengali। Class xii derivatives।for more videosLink for Class xii limithttps//youtube/ZCQwxOkK2OcLink for class xii limithttps//yo



Implicit Differentiation



Implicit Differentiation Notes Cocalc
It means that I need to differentiate the equation one time to find y ′ and then once more to find y ″ The correct answer from the textbook is y ′ = x 1 y and y ″ = x 2 2 x y 3 I got the first derivative right, but I can't understand how did they get the second one, or is it a typo (unlikely), since I have y ″ = 1 y − ( x 1In calculus, the second derivative, or the second order derivative, of a function f is the derivative of the derivative of f Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; The derivative of #g(x)# is #2# and the derivative of #h(x)# is #2x# We can now substitute into the formula and calculate Note the notation #y''# is used to show that we're finding the second derivative, and not the first, as would the notation #y'# Similarly, #y'''# would signify the third derivative #y'' = (2 xx x^2 2x xx 2x)/(x^2)^2# #




If X 2 Y 2 25 Then Find Dy Dx
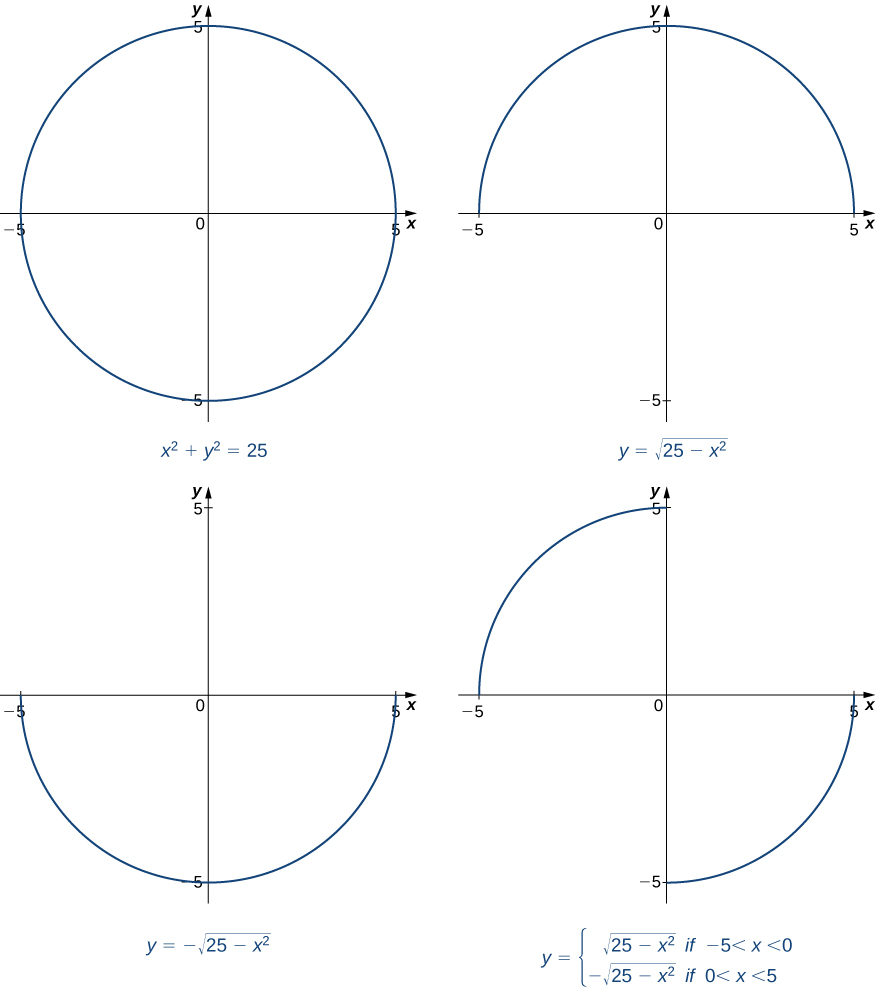



3 8 Implicit Differentiation Calculus Volume 1
However, I thought the second derivative was supposed to be $\frac{3}{2}\sec^2(t)$ What am I doing wrong? Find the first and second derivatives involving differences, products, and quotients \(\displaystyle{y}={\frac{{{\left({x}{1}\right)}{\left({x}^{{{2}}}{x}{1What's the derivative of mathx^2y^2=a^2/math?



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Q4 Pdf




Implicit Differentiation
Example using implicit differentiation to get the second derivative of y wrt x Uses substitution to get final expressionThis video screencast was createdFind dy/dx x^2y^2=25 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Since is constant with respect to , the derivative of with respect to is Reform the equation by setting the left side equal to the right side Solve for Tap for more steps




Intuition Behind Implicit Differentiation Of X 2 Y 2 25 Youtube



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch03 Pdf




X 2 Y 2 25 Novocom Top




Implicit Differentiation



Math 112 Calculus I Final Exam Solutions 1 25 Points The Figure



Business Calculus




Difrentiation Phpapp01



What Is The Solution To X 2 Y 2 25 Xy 12 Quora




Oneclass 1 Find The Second Derivative D 2y Dx 2 As A Function Of X And Y X 2 Y 2 25 2 F




Curve Sketching




The Angle Between The Curves X 2 Y 2 25 And X 2 Y 2 2x 3y 43 0 At 3 4 Is




Express X Y X 2 Y 2 25 Where X Y Inw As A Set Of Ordered Pairs



4 2 Implicit Differentiation



4 2 Implicit Differentiation



Worked Example Evaluating Derivative With Implicit Differentiation Video Khan Academy



Implicit Differentiation




Find The Point Of A Intersection Of Circle X 2 Y 2 25 And Line 4x 3y 12 And Also Find Length Of Intersecting Chord




Warm Up 10 3 13 1 The Graph Of The Derivative Of F F Is Given Which Of The Following Statements Is True About F A F Is Decreasing For 1 X Ppt Download



What Is The Solution To X 2 Y 2 25 Xy 12 Quora




Example 17 Find Points On X2 4 Y2 25 1 At Which Tangents




How To Draw Y 2 X 2




Problem Of The Day If X 2 Y 2 25 What Is The Value Of D 2 Y At The Point 4 3 Dx 2 A 25 27 C 7 27 E 25 27 B 7 27 D 3 4 Ppt Download



3 8 Implicit Differentiation Calculus Volume 1



2 6 Webassign Answers




If A X Y X 2 Y 2 25 And B X Y X 2 9y 2 144 Then A B Contains




Rd Sharma Class 12 Solutions Chapter 18 Maxima And Minima




Implicit Differentiation




Find The First And Second Derivatives Of The Chegg Com




Y V1 X2 1 31 2 X Y 2 25 X Y 3 1 Chegg Com



Intuition Behind Implicit Differentiation Of X 2 Y 2 25 Youtube




Find The Derivative Of X 2 Y 2 25 Using Implicit Differentiation Youtube




If The Circle X A 2 Y 2 25 Intersect The Circle X 2 Y B 2 16 In Such A Way That Common Chord Is Of Maximum Length Then Value Of A 2 B 2 Is



1




How Do You Find Equation Of Tangent To Circle X 2 Y 2 25 At The Point 3 4 Socratic




Solution Find The Second Derivative Of Y By Implicit Differentiation




Answered Find All Relative Extrema Of The Bartleby



3 8 Implicit Differentiation Calculus Volume 1



Numeracy Maths And Statistics Academic Skills Kit



For Curve X 2 4 Y 2 25 1 Find Those Points Where Tangent Is Sarthaks Econnect Largest Online Education Community
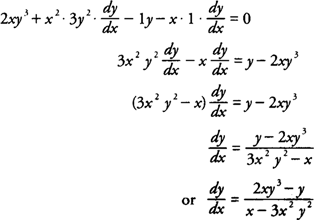



Implicit Differentiation




Oneclass 1 Find The Second Derivative D 2y Dx 2 As A Function Of X And Y X 2 Y 2 25 2 F



3 8 Implicit Differentiation Calculus Volume 1




Can You Find The Point In The First Quadrant On The Lemniscate 2 X 2 Y 2 2 25 X 2 Y 2 Where The Tangent Is Horizon X And The Value Of Y Is Unknown Quora



3 8 Implicit Differentiation Mathematics Libretexts



1



Chain Rule




1 Implicit Differentiation 2 Introduction Consider An Equation Involving Both X And Y This Equation Implicitly Defines A Function In X It Could Be Defined Ppt Download



Solved 9 Find The Second Derivative Of The Function 4 10 X Y 2 X Oa D Y 2 X Dx 2 X D Ob D Y 60 Dy Course Hero
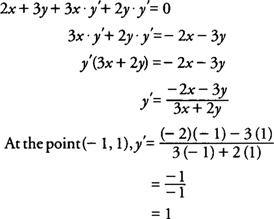



Implicit Differentiation



Page 7 Differential Calculus High Resolution Stock Photography And Images Alamy




5 Create A Matlab Script To Find The First And Second Derivative Of Given Function Using Forward Backward Central An Homeworklib




Solution Find The Second Derivative Of X 3 5x 2 X 0




3 Derivatives Derivatives The Functions That We Have




Find The Volume Of The Solid Generated By Rotating The Region Bounded By The Curves X 2 Y 2 25 X 8 About Y Axis Study Com




X 2 Y 2 25 Novocom Top



4 2 Implicit Differentiation
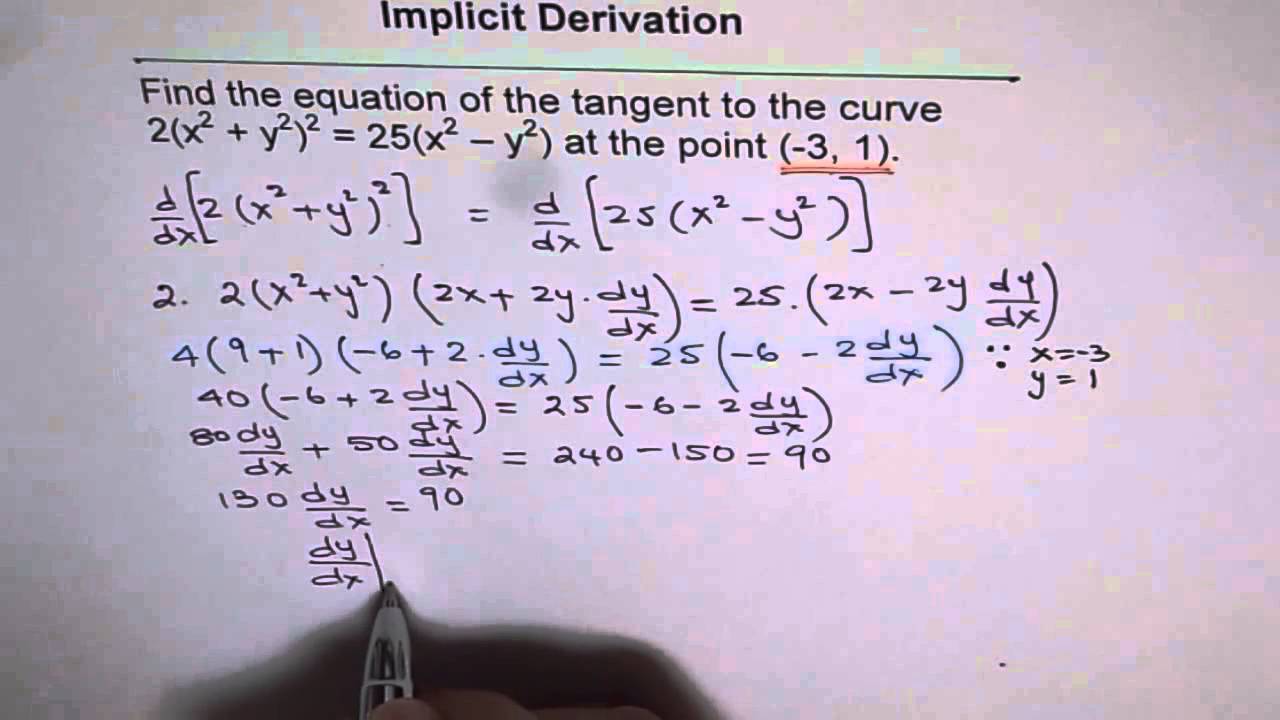



Equation Of Tangent To 2 X 2 Y 2 2 25 X 2 Y 2 Implicit Differentiation Youtube




Problem Of The Day Calculator Allowed Ppt Download



The Equation Of A Circle Is X 3 2 Y 2 2 25 How Do You Show That The Point A 6 6 Lies On The Circle And Find The Equation Of The Tangent
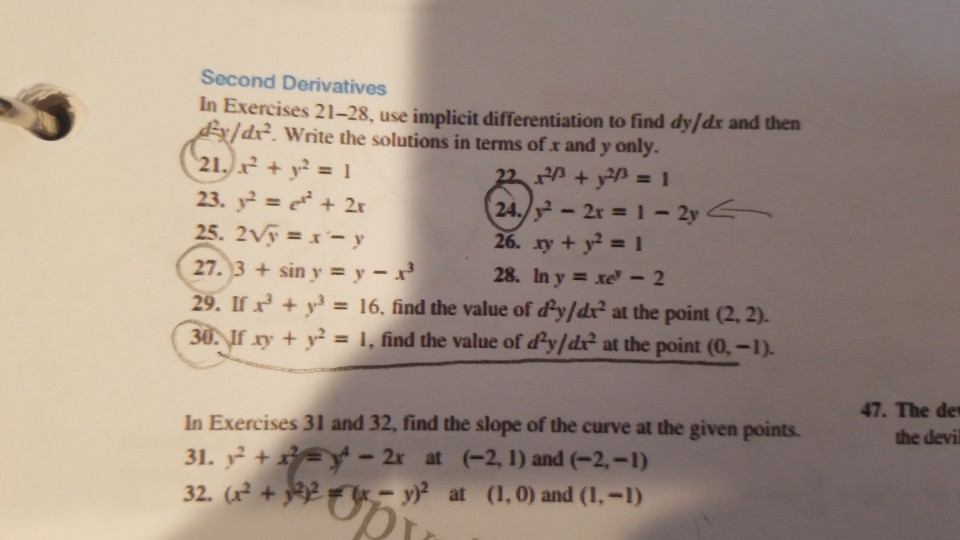



Second Derivatives In Exercises 21 28 Use Implicit Chegg Com



4 2 Implicit Differentiation




Solved Find The First And Second Derivatives Of The Funct Chegg Com




Chapter Applications Of The Derivative




A First Course In Elementary Differential Equations Problems And Solutions Marcel B Finan Arkansas Tech University C All Rights Reserved Pdf Free Download




Unit 2 Lesson 9 Implicit Differentiation 1 2 So Far We Have Been Differentiating Expressions Of The Form Y F X Where Y Is Written Explicitly In Ppt Download
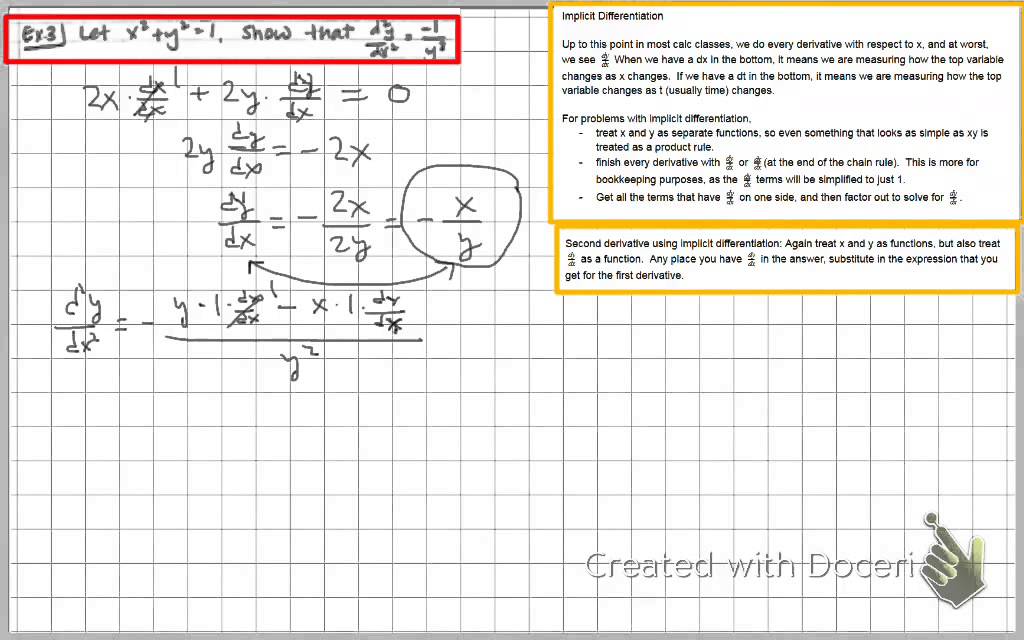



Calculus Find Second Derivative Of X 2 Y 2 1 Youtube



2 6 Webassign Answers




Motion Along A Curve Finding Rate Of Change Video Khan Academy
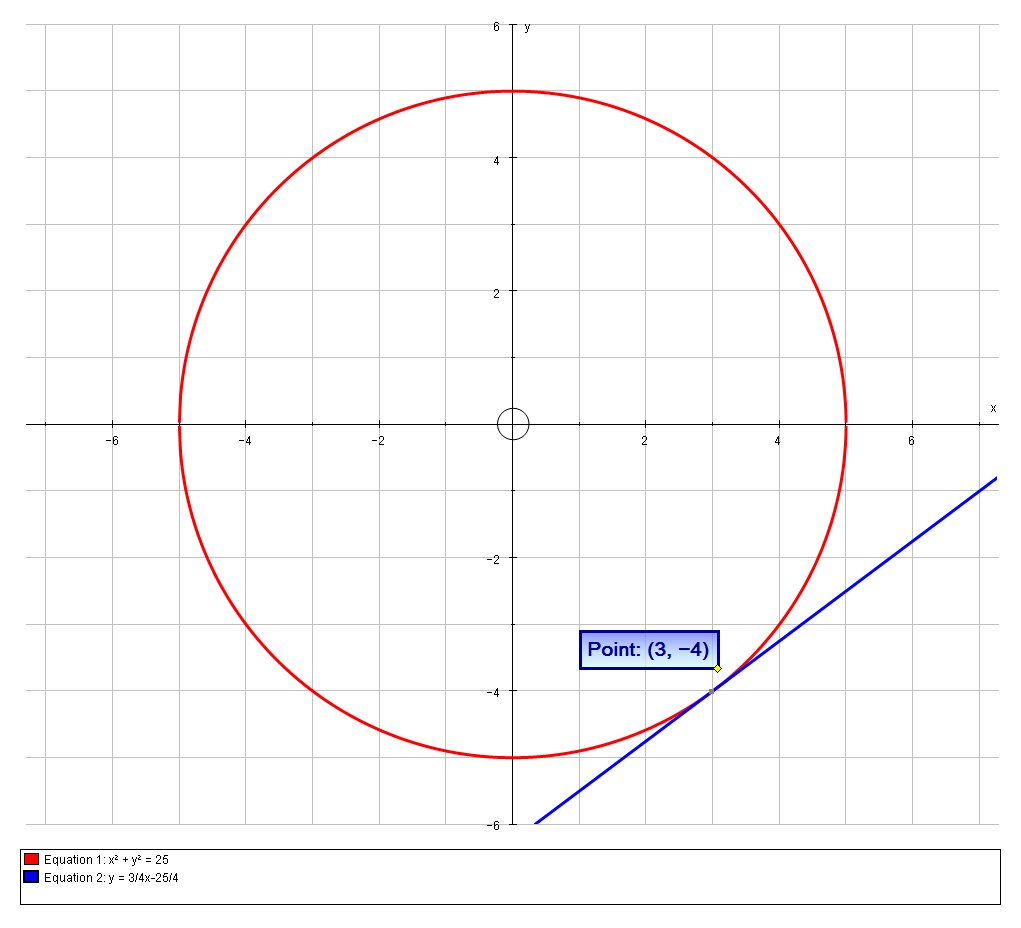



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic




Ab Is A Chord Of The Circle X 2 Y 2 25 The Tangents Of A And B Intersect At C If 2 3 Is The Mid Point Of Ab Then Area Of The Quadrilateral Oacb Is



Tangent And Normal Lines Page 2




However Some Functions Are Defined Implicitly Some Examples Of Implicit Functions Are X 2 Y 2 25 X 3 Y 3 6xy Ppt Download



Implicit Differentiation Notes Cocalc




X 2 Y 2 25 Novocom Top




Given The Curve X 2 Y 2 25 Find To Three Decimal Places The Value Of The Second Derivative When X Youtube




Example 17 Find Points On X2 4 Y2 25 1 At Which Tangents
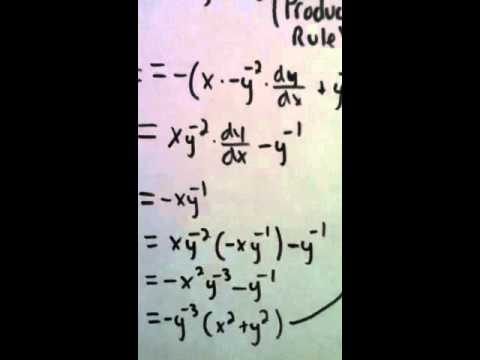



How To Find D 2y Dx 2 Of X 2 Y 2 4 Youtube




Implicit Differentiation Mastery For Chain Rule U Substitution And Implicit Differentiation Quiz And The Chapter 3 Test Abby S Calc Blog




1 Implicit Differentiation 2 Introduction Consider An Equation Involving Both X And Y This Equation Implicitly Defines A Function In X It Could Be Defined Ppt Download




2 Differentiation 2 1 2 2 2 3



0 件のコメント:
コメントを投稿