円柱の体積は、円の断面積と高さを掛けて算定できます。 容積= (10)/2cm× (10)/2 cm×314×10 cm =785cm3 = 785ml 計算自体は簡単ですね。 さいごは容器でよく使う単位に訂正してくださいね。 ※体積の単位は下記の記事が参考になります。 体積と重量の違いは円筒座標系から直交座標系へは以下のように変換できます。 Ansysにおける取扱い Ansysで円筒座標系を参照した場合でも、座標軸はX,Y,Zで表記されますので、XはR、Yはθと読み替えてください。 関連用語 直交座標系、 極座標系正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積

中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
円筒の体積 斜め
円筒の体積 斜め-Jzj 5 p 4a2 x2 y o と表される.ゆえに, Vol(E) = ZZZ E dxdydz = ZZ fx2y25a 2g dxdyこの場合,回転体は半径2cm,高さ4cmの円柱になるので,その体積Vは V=底面積×高さ=2×2×π×4= 16π cm 3 となります. これをパップス・ギュルダンの定理を使って解いてみます. 「 断面積 」は縦4cm,横2cmの長方形なので 2×4=8 cm 2 です. 「 断面の




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
体積を求めるには、底面となる円の面積を積分してもよい。 V = ∫ 0 h π ( r 1 − r 2 h x r 2 ) 2 d x = π h 3 ( r 1 2 r 1 r 2 r 2 2 ) {\displaystyle V=\int _{0}^{h}\pi \left({\frac {r_{1}r_{2}}{h}}xr_{2}\right)^{2}\,dx={\frac {\pi h}{3}}(r_{1}^{2}r_{1}r_{2}r_{2}^{2})} · 円筒(えんとう)とは。意味や解説、類語。1 まるい筒。2 ⇒円柱2 goo国語辞書は30万4千件語以上を収録。政治・経済・医学・ITなど、最新用語の追加も定期的に行っています。円筒 パイプ 体積計算 公式 求め方 チューブ 高さ 長さ 外径 内径 自動 volume
図44 円筒座標系における微少体積と面ベクトル 方向の面積積分を考えてみよう.面ベクトルは dS 1 = a dS =a ( d ) d dz ,dS 2 =–a dS – =–a d dz (421) なので,この2面の積分は次のように書くことができる. AA ⋅ dS 1 1 A ⋅ dS 2 2 = A d a a dS A – a a dS – = A1. 直円柱 r = 半径 d=直径 h=高さ 2. 中空円柱 r = 中空部半径 R=半径 h=高さ 3. 斜切円柱円筒導体の外側表面は、接地されており、電位は'0'である。無限の遠方でも電位は'0'であるから、円筒導体の外側表面には電荷は分布しない。 ② ①において、円筒導体1の中心軸からの距離rmにおける電界の大きさを求めよ。 答
数学用語。円筒ともいう。平面上に,平行な2直線 l,gをとり,lを軸としてこの平面を回転させるとき,gがつくる曲面 (回転面) を円柱という。内部も含めたものを円柱ということもある。 l,gは,それぞれ円柱の軸,母線 (すべての位置について) と呼ぶ。円柱を軸に平行でない平面πで切取っ円柱の体積 π×3 2 ×4=36π (cm 3)からくぼみになっている円錐の体積 π×3 2 ×4÷3=12π (cm 3)を引くと V=24π (cm 3) 8 AB=3cm,BC=4cm,CA=5cmの直角三角形を,図のようにBCから3cm離れた直線DEの周りに1回転させとき, ABCが通ったあとにできる立体の体積は (cm 3 )円筒状のポリ袋の断面積は一定であるとみなせることから,体積の代わりに円筒の長さを用いると次 のようになる。 Pvap = { (Lt-Lair) /Lt }× P Lair:空気の採取後の円筒長さ Lt :有機溶剤の蒸発・平衡後の円筒長さ 2実験装置




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
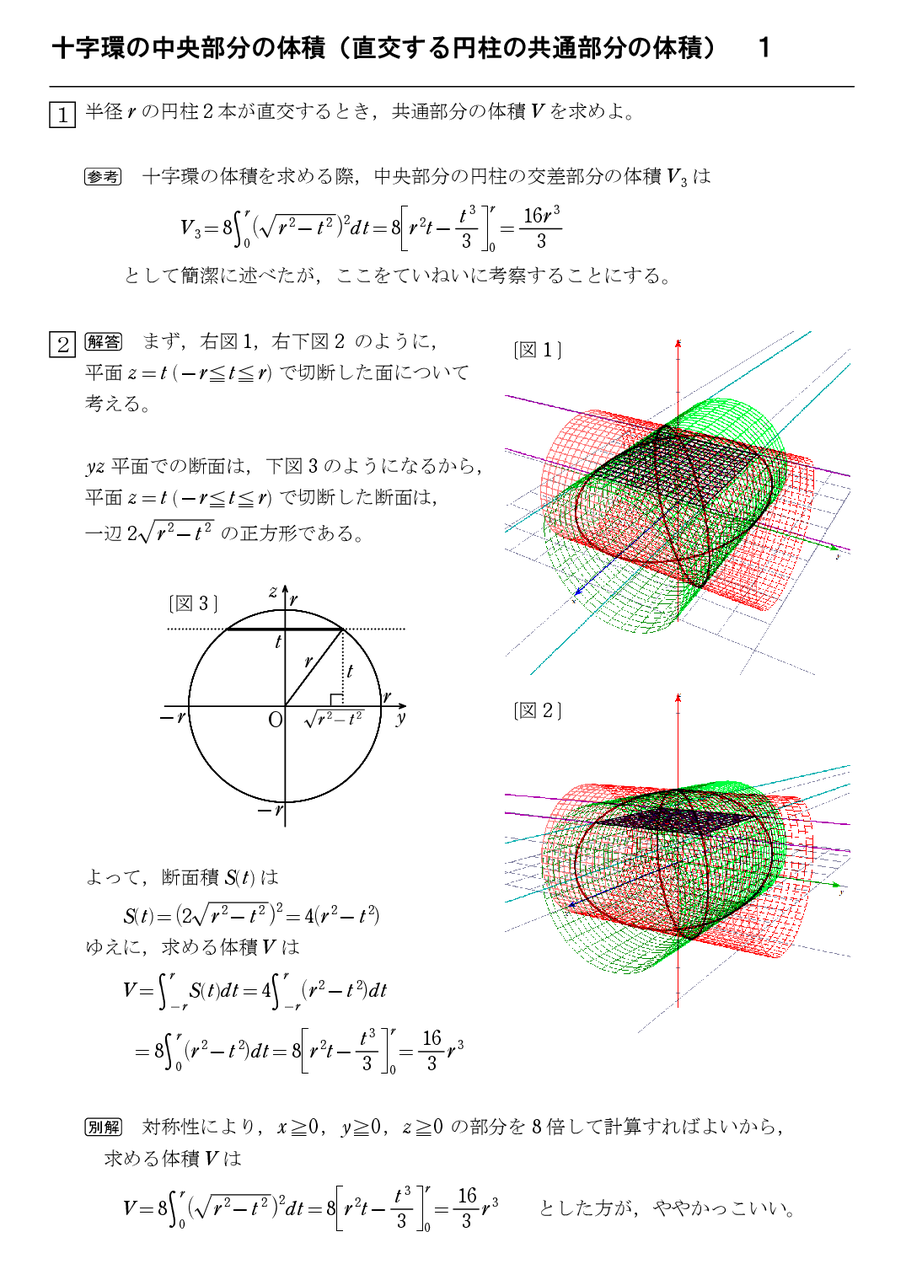



十字環の中央部分の体積 直交する円柱の共通部分の体積 1 怜悧玲瓏 高校数学を天空から俯瞰する
1227 · 1)75・75・314・90= (cc)= (L) 2)75・75・314・100= (cc)= (L) 3)75・75・314・1= (cc)= (L) · 円筒座標系 線素および体積要素 円筒極座標系を含む多くの問題においてがこの座標系でどのように表されるかを知っていることは有意である(それにより曲線経路や体積を含む問題を積分によって解く方法が考えら熊本大学数理科学総合教育センター 3(9)(立体の体積2) 球x 2y z 25 4a2 と円柱x y2 5 a の共通部分E の体積を求めよ. 解 x 2y z2 5 4a 2よりjzj 5 p 4a x2 y2 だから, E = n (x;y;z) x 2y2 5 a ;



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の内容積の求め方 あるテストの問題で 円柱の内容積を求めよとあ 数学 教えて Goo
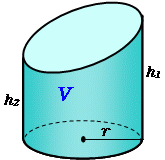
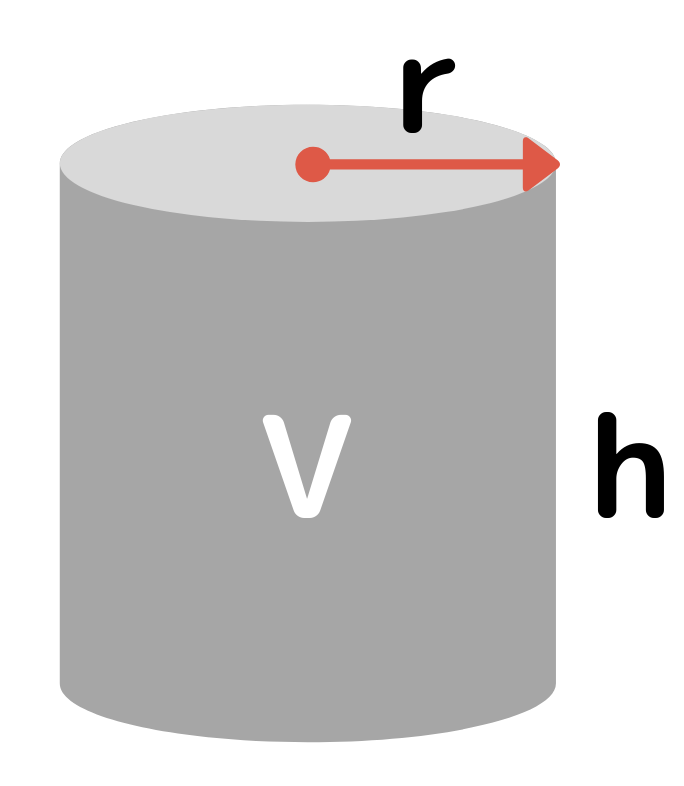
み合わせ円筒"が有効である.図23に示した組み合 わせ円筒では,内側円筒の外径が外側円筒の内径より も大きいために,圧入した状態では内側円筒には外圧 σz σz σθ σθ d t σ θt σt p d dθ p d 2 dθ t (a) (b) の計算式の導出σθ θ 図22 内圧を受ける薄肉円筒1 第1章 基礎事項 11 微分積分 偏微分 変数x, y, z の関数f = f(x,y,z)について ∂f ∂x) yz = lim ∆x→0 f(x∆x,y,z)−f(x,y,z) ∆x (11) をf のxによる1階の偏微分という y, z による偏微分についても同様に 定義する ここで, 左辺の()につけた添え字yz は偏微分を行うさいにy, z を一定とみなすことを意味する円柱 円柱の体積を求める公式は、次の通りです。 V = Sh = πr2h V = S h = π r 2 h ここで、V は円柱の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円柱の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円柱 P12
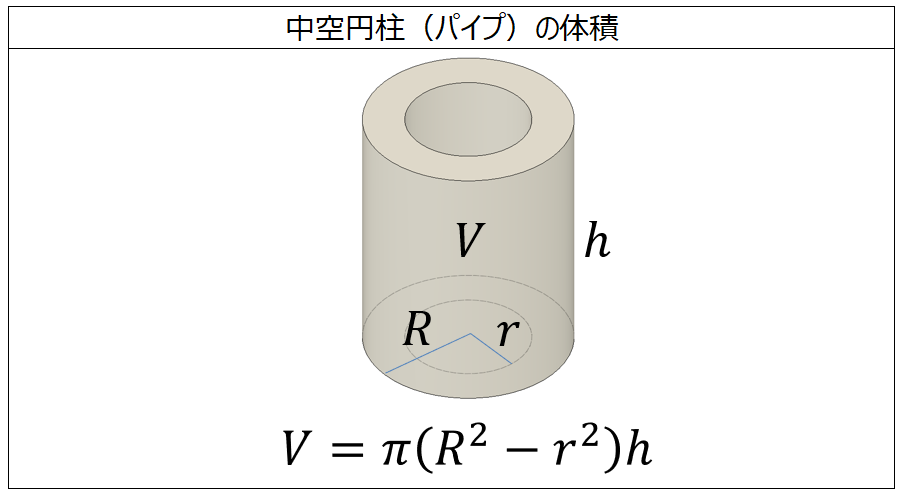



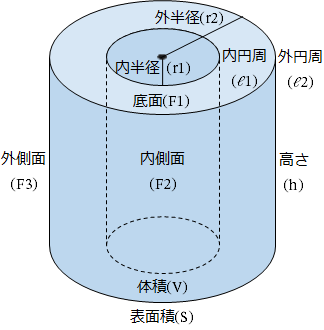
体積の計算 中空円柱 パイプ 製品設計知識
_中空円筒の体積 is _円周率×_高さ×(_外径の2乗 _内径) 円周率() 中空円筒の体積(_高さ,_外径,_内径,_中空円筒の体積) 円周率(_円周率), _中空円筒の体積 is _円周率 * _高さ * (_外径 ^ 2 _内径1803 · 円柱の体積を求める方法 円柱の体積を求める方法は とーーーーっても簡単です。 底面積×高さ これだけ! · θを求めるには θ= acos (h/r) を使って計算します。 (acosは逆三角関数 (arc cosine)です。 )これで普通の関数電卓かexcelで計算できる式になりました。 このTに円柱の高さをかけ算すると、体積が求められます。 もし半分より多く水が入っている場合は、(上記の計算では水のない部分のDの字型の面積を求めたので)Tの代わりに2πr^2からTを差し引いたものを




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
· 円柱の体積の求め方はむちゃくちゃ簡単。 底面積×高さ っていう公式をつかえば、一発で体積を求めることができるんだ。 そんで、 底面積は、 半径×半径×円周率 だから、円周の体積はつぎの計算式で求められるよ。 半径×半径×円周率×高さ以下の (1) 直交座標系はもちろんですが、 (2) の円筒座標系、 (3) の球座標系も、座標軸は互いに垂直になります。 簡単な場合で、原点を O として、高校数学に出てくる極座標系 で考えます。 , が成り立ちます。 直交座標系で x , y の関数として と表さ1929 · このようにして,錐体の体積を求める公式を知っていれば,小学六年生でもこの立体の体積を求めることができる. 図3 全く同様にして,カヴァリエリの原理により,半球の体積を「円柱から円錐を引いた図形」の体積に帰着させて求める事ができる.これについては図を掲げるだけに




切断された物体の体積 画像のように 半径aの円柱を切断 その体積を求めた Okwave



1
円柱の体積 V は、 円周率× 半径 × 半径 × 高さ便利な計算フォーム 建設施工 測量計算 安全 :玉掛け、潜水時間 コンクリート :材料、鉄筋、型枠、維持管理等 構造 :断面、型枠支保工、梁、土留等 土質 :スウェーデン式、コーン貫入等 水理計算 :管、仮設、水替 · 1 円筒胴の場合 2) 図1に示す円筒モデルに, p が作用している状態を想定する。 応力( σ )は荷重( l )を断面( a )で除して得られるが,円筒胴の場合,次の2つがある。 1)軸(長手)方向応力: σ 1 σ 1 は,軸方向(周断面)に働く応力である。
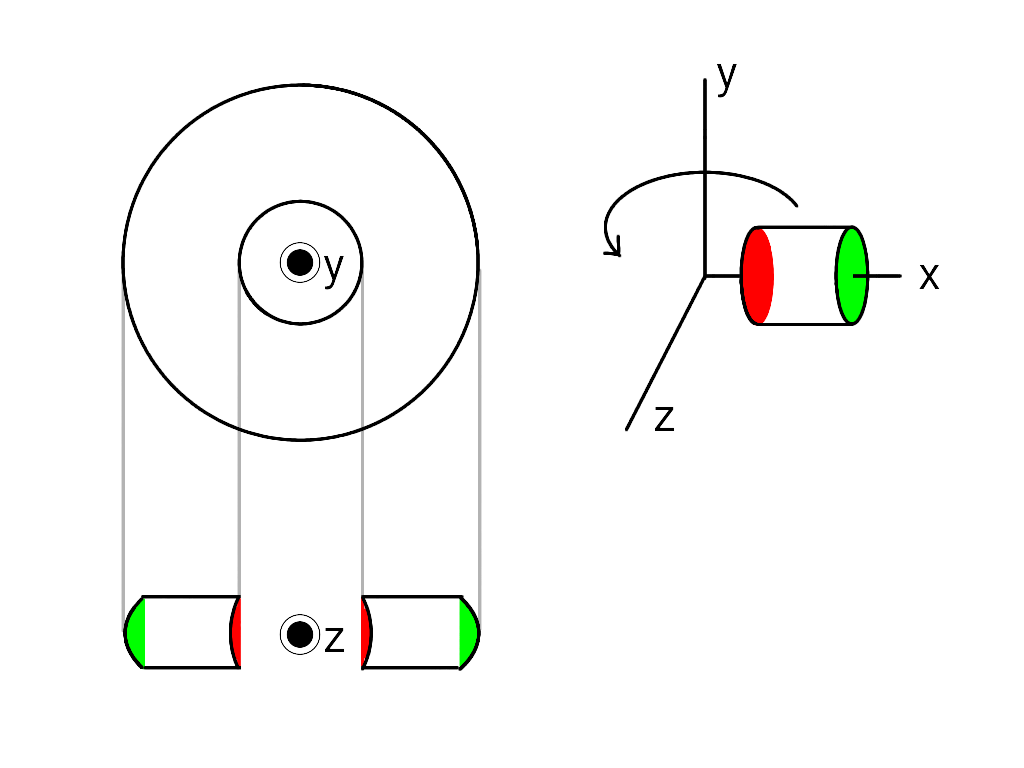



図解 円筒の回転体を図示してみよう 東北大07 名古屋大11 理系のひとりごと




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
7定積分 (回転体の体積) 小学校や中学校で, 三角すいの体積 三角すいの体積: 球の体積: であることは,学習したと思います。 その時,「どうして円すいの体積が,円柱の体積の3分の1になっているのか? 」,また,「どうして球の体積は,この上記の(解)では、体積 V の最大値を求めるために微分法を活用したが、微分を用いず に、次のような計算をしても求められることに驚かされる。 V-2πk 3 =-π(r 3 -3k 2 r+2k 3 )=-π(r-k) 2 上記の不等式から、体積 V は、 r=k のとき最大で、最大0703 · 円筒の体積の計算式ってどうなるのでしょうか? 円筒が円柱の意味だったら、底面積×高さです。 底面の円の半径がr、高さがhだったら、πr^2hです。




円柱の表面積の求め方 公式と計算例
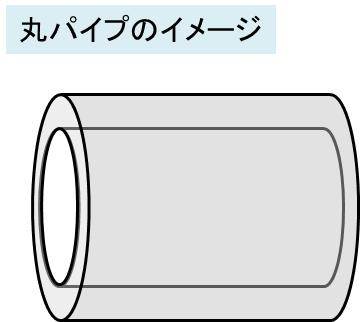



丸パイプ パイプの体積と重量計算方法 鉄 ステンンレス 銅の場合
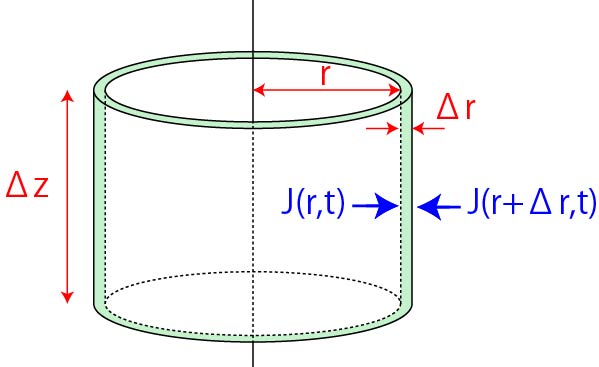
円柱座標 3次元の場合,Pからxy平面に下した垂線の足P'の極座標と,PP'(つまり,z軸)を座標とすることができます.この座標は (r,φ,z)で,これと (x,y,z)との間には, の関係がある. · 日本語で「円筒」と言うと,普通は中身が空洞になっているものだろう.きっと日本人ならそう思う.だって「筒」自体には中空であることが定義に含まれているのだし. ところが「円筒」と辞書 1 で調べてみると, まるい筒。 ⇒円柱2 とある.第一義円筒自体の体積ΔV,面積ΔSin,ΔSoutはそれぞれ, と近似できるので, となります.Δrが十分小さいときには, となります.これが 円筒における 拡散方程式 です. 次に, 球殻 における拡散の様子を考えていきましょう.




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
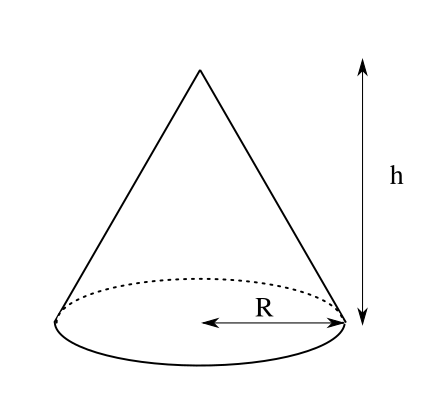



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目
錐体の体積の場合は、b=0で、c=a/4 (2乗に比例する)だから、 そうすると、4次元錐体の体積は、b=0で、c=a/8 (3乗に比例する)だから、 となるはず。 s:へー。あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体Grapes3D利用して,実モデルではなく,図を次のように表した。 前回のレポートで,円柱の45°切断という,いわゆる非回転体の求積問題について,次のページのような問題を考えたが,その立体の"全体図"を考えたようなものと想像していただければと思う。 本レポートでは,計算の便宜上,半径1の円の底面をもつ,高さ2の円柱を切断することにする。 (1) 体積に



Excelワークシート 中空直円柱の体積や質量などの物理量を計算するワークシート 黒い箱の中



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
熱 膨 張 率 気体は、熱を加えると分子の運動が激しくなり、体積が大きくなる ことは シャルルの法則 で勉強しました。 固体も同じで、分子間の距離が増大して、膨張します。 一般的に 次のような関係が成り立ちます。 αは 線膨張率 で温度差1Kあたり




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
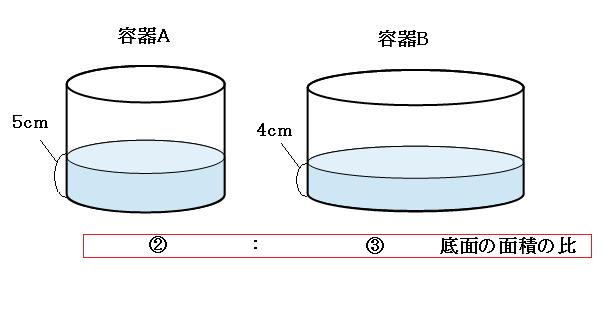



体積と比の問題の解き方 底面積の比と深さの比は逆になる




3月4日はバウムクーヘンの日なので 積分します 理系男子の独り善がり




球の表面積と体積の公式 数学fun




中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
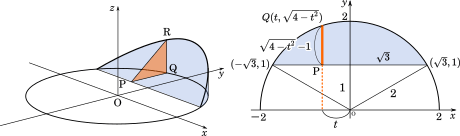



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書




空間図形14 円すい台の体積 Youtube




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
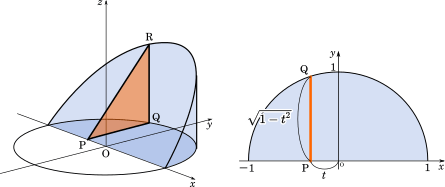



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書




円柱の展開図 Youtube



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係




体積の求め方 計算公式一覧



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



いろいろな立体の問題



円筒の体積計算 デジタル教科書 電子教科書
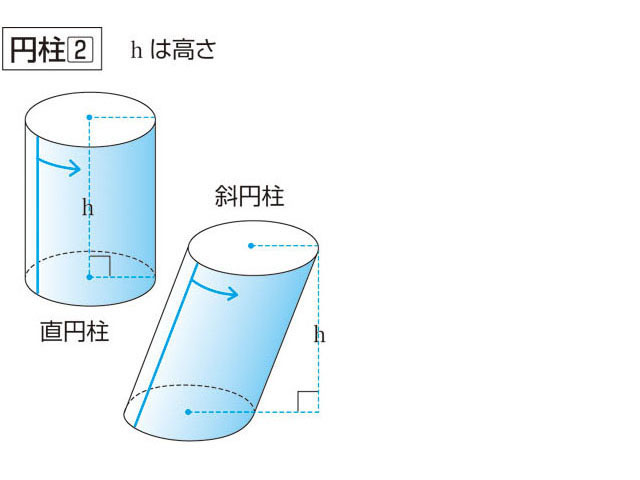



円柱とは コトバンク
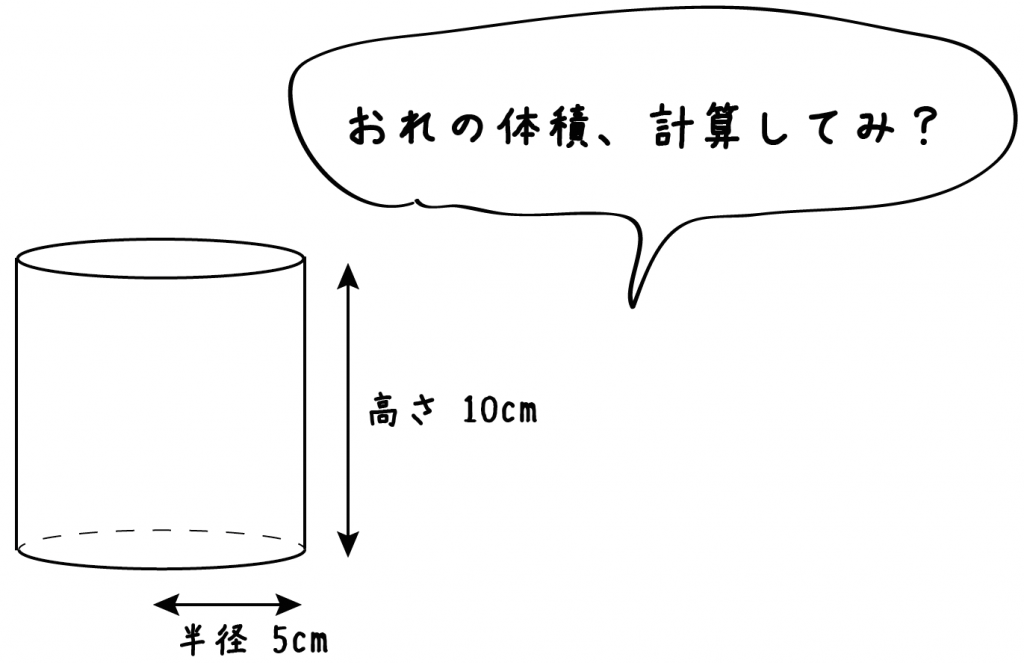



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
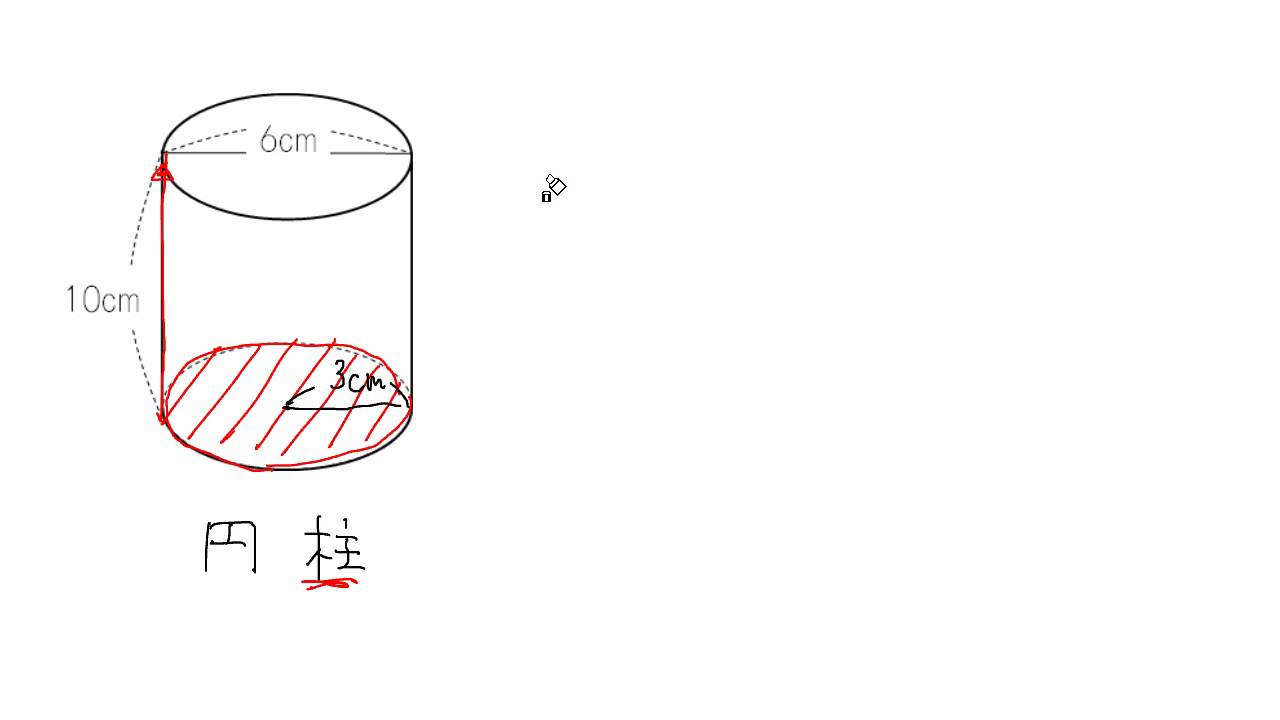



円柱の体積 Youtube



3



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
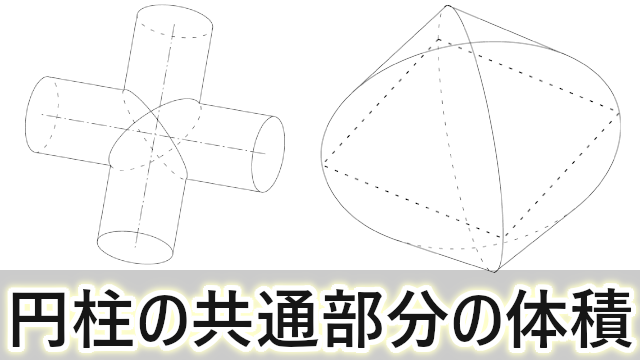



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法
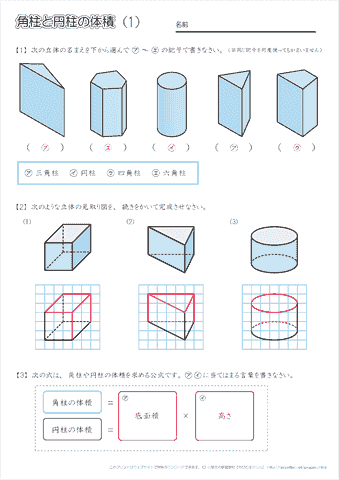



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
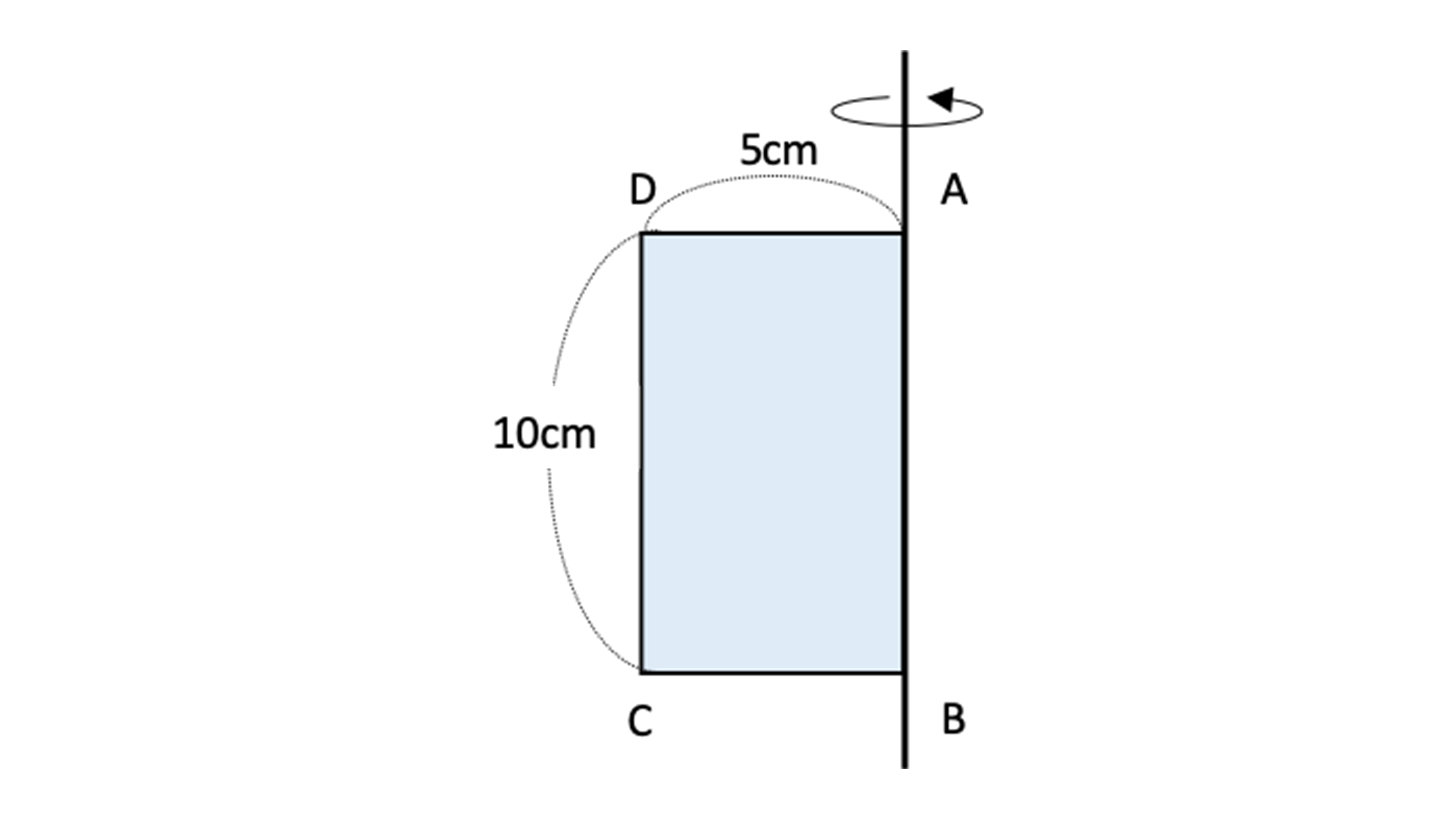



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



1




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
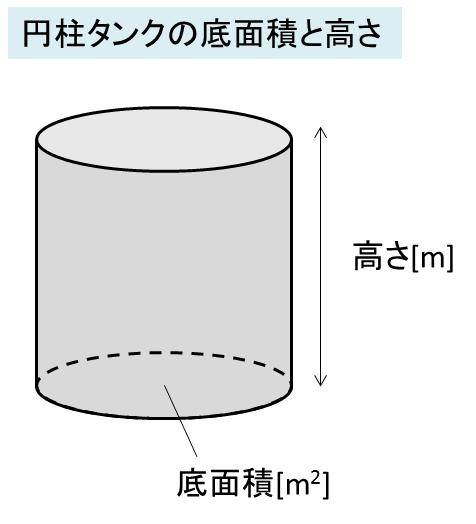



燃料タンクなどの円筒型タンクや角タンクの容量の計算方法




高校数学 不等式で表された立体の体積 直交する円柱の共通部分の体積 受験の月



無題ドキュメント
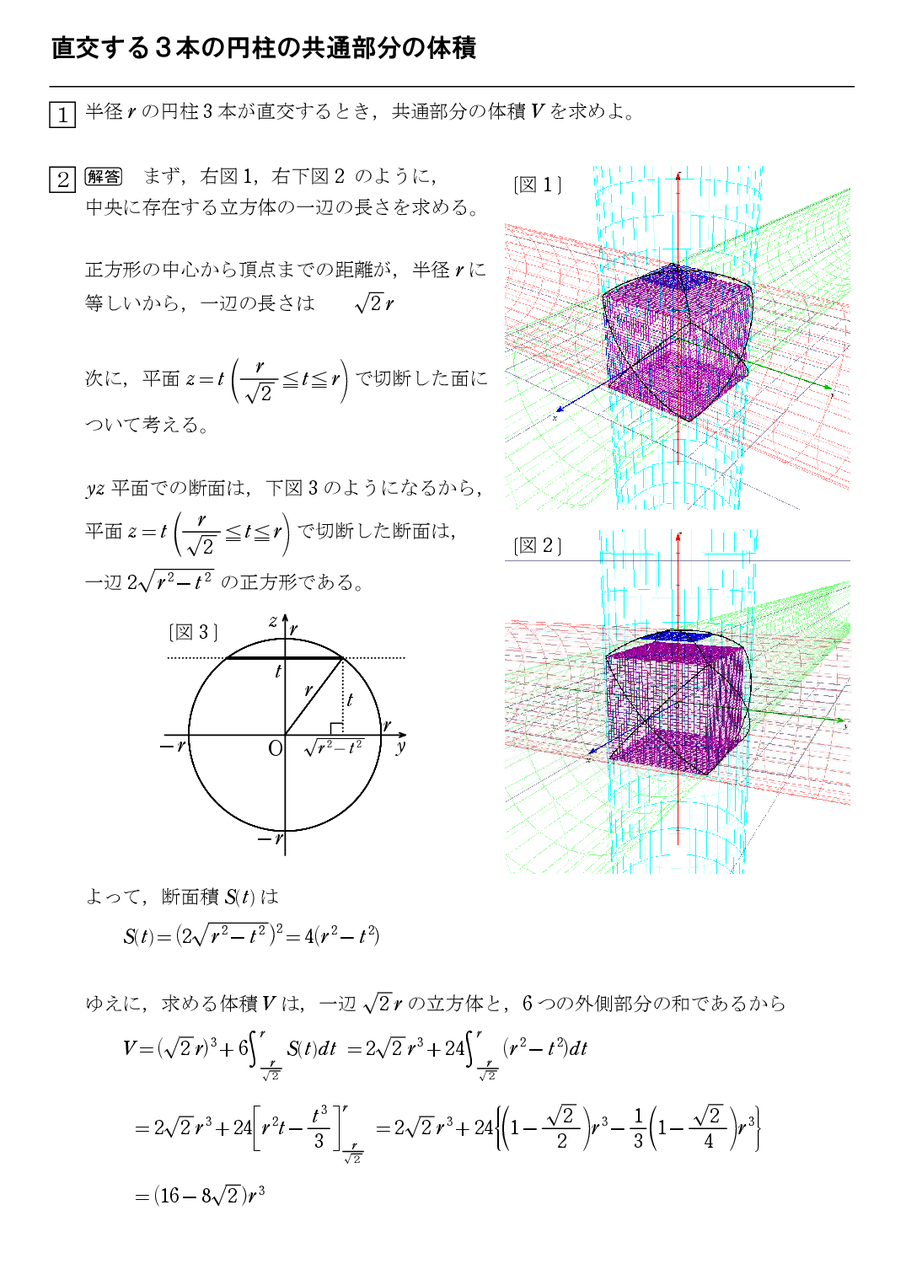



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



体積の計算 中空円柱 パイプ 製品設計知識



質量と比重



Excel関数 直円柱の体積や表面積を計算するrccylinderカスタムワークシート関数群 黒い箱の中




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
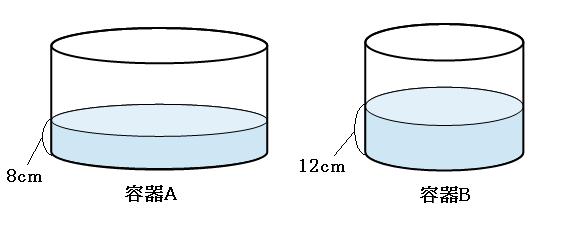



体積と比の問題の解き方 底面積の比と深さの比は逆になる
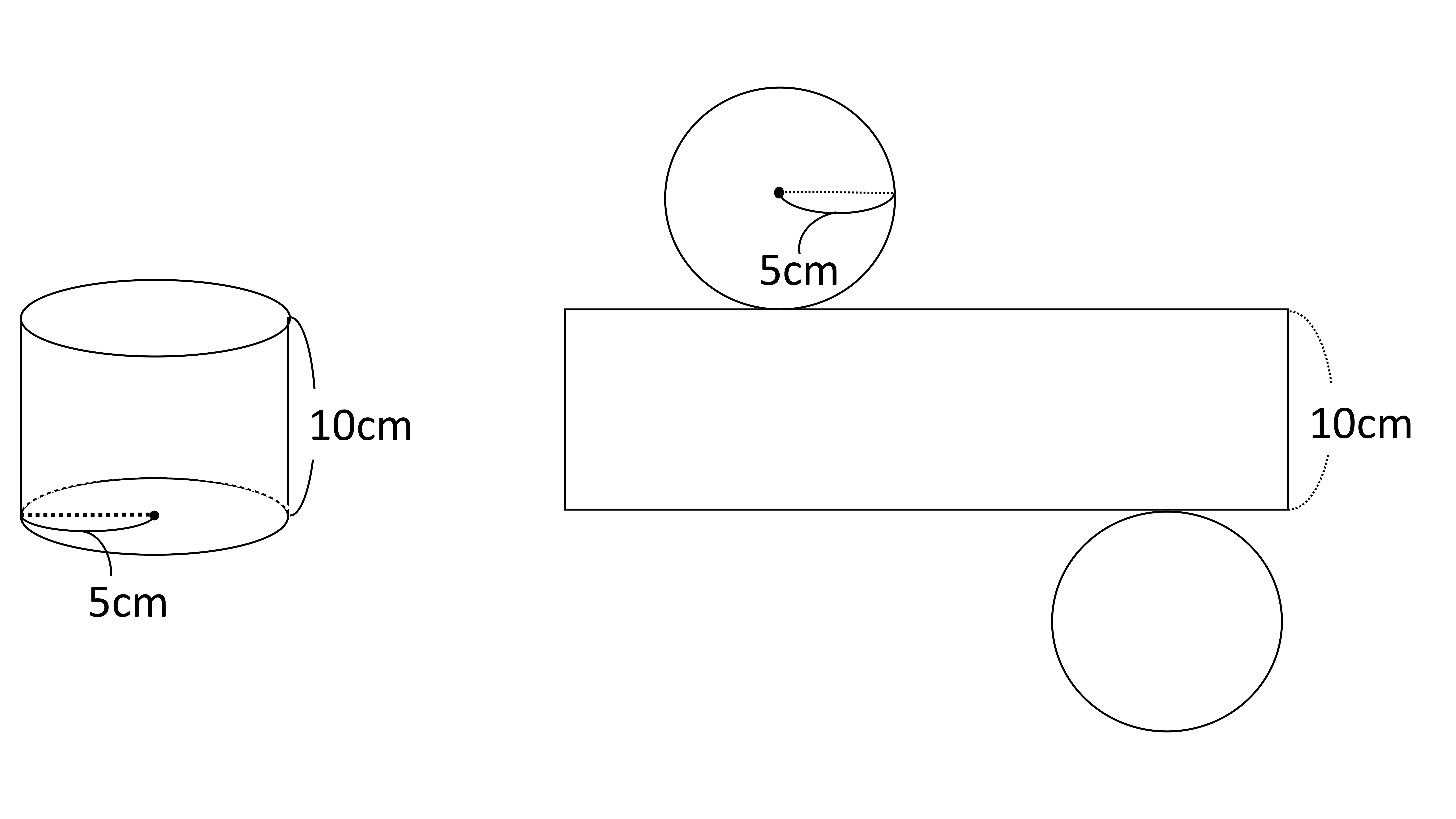



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



斜切円柱の体積 高精度計算サイト



円柱の体積の計算フォーム 直径 高さ Cm 体積 リットル を算出 寝袋 シュラフのプロが極秘で教える 失敗しない選び方 使い方



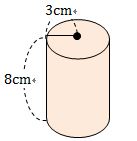
円柱の体積




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
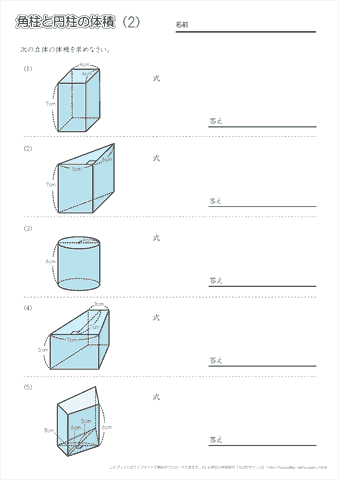



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生



いろいろな立体の問題




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル



写真のような円柱の体積を 微小体積要素 Dv Rdrd8dzを積分して求めたい Yahoo 知恵袋
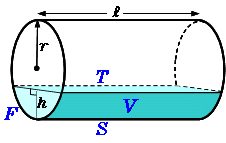



一部が欠けた直円柱の体積 高精度計算サイト
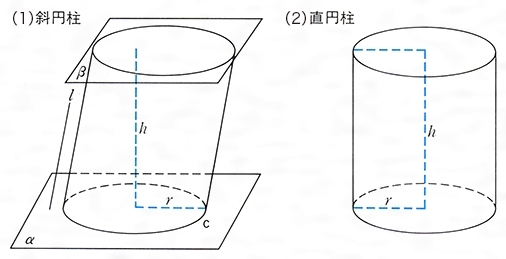



円柱とは コトバンク



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




高校数学 体積の計算 1 問題編1 映像授業のtry It トライイット




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学 円筒分割積分 バウムクーヘン分割積分 V 2p Xf X Dx 受験の月
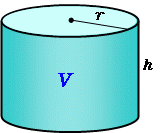



直円柱の体積 高精度計算サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す
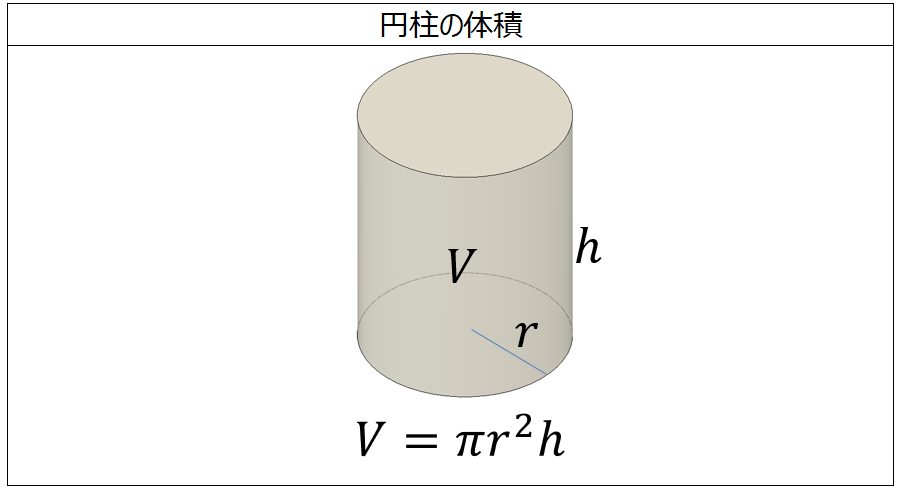



体積の計算 円柱 製品設計知識
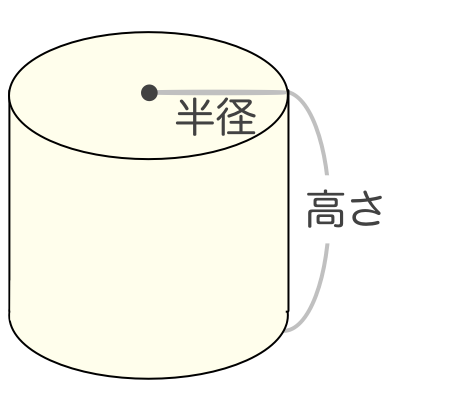



円柱の体積 簡単に計算できる電卓サイト



技術資料 立体の体積
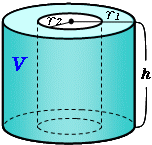



中空円柱の体積 高精度計算サイト




円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の展開図 Youtube




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



円柱の斜め切断
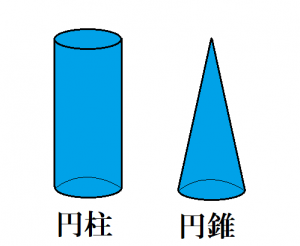



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




円柱の体積の求め方 公式と計算例



円筒 パイプの体積と公式 体積計算機




球の表面積と体積の公式 数学fun




円柱座標系でのbの積分区間が2枚目のようになるのがわかりません 教えてください Clear




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係




円柱の表面積と体積を求める公式 具体例で学ぶ数学




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
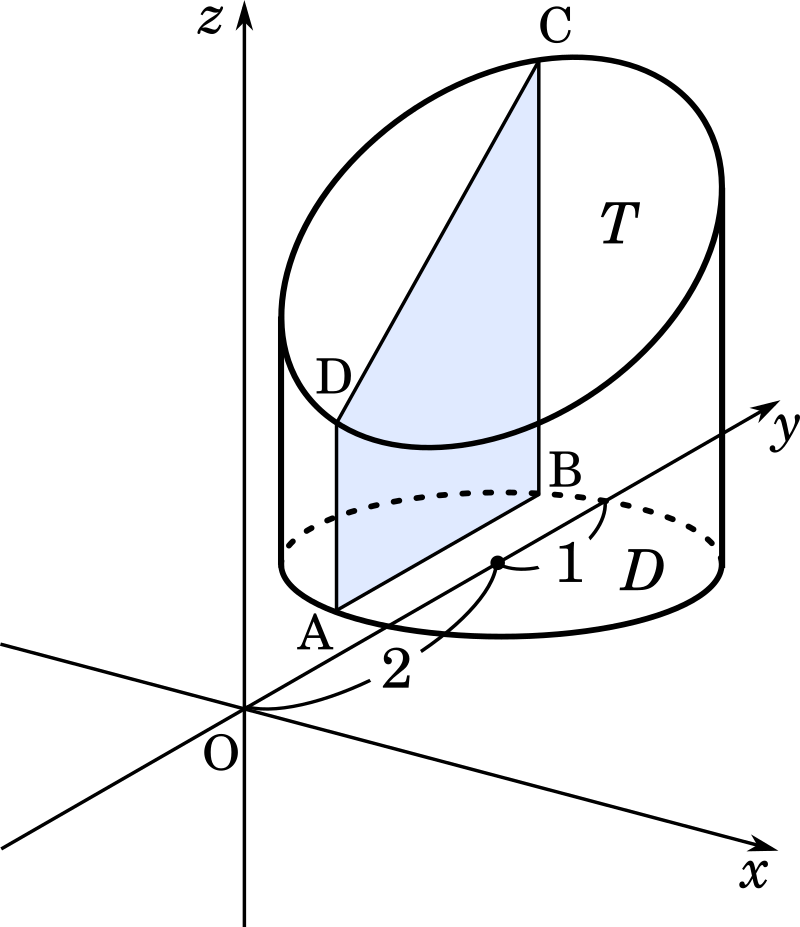



数iii積分 円柱を斜めに切った体積とドーナツ回転体 断面が台形 九州大 Mm参考書




円柱の表面積と体積を求める公式 具体例で学ぶ数学



0 件のコメント:
コメントを投稿